______                     
                 /      |       ________     
                /       |____  /        \    
               /        |    \/   _      \   
               \       ___       /_\      \  
                \      \_/          .      \ 
                 \          /\_____/       / 
                  \________/      |       /  
                                  |______/   

I needed to load some .dol files on my GameCube and was advised to get one of these third party SD card readers for the console. After searching a bit, I learned that the GC memory card system is in fact a modified SD card reader and as a consequence it is possible to use an existing memory card and fit it with an SD card socket.

I did not have such a socket but I thought I could directly use instead a spare SD to Micro SD adapter and wire its pins directly on the pins from the memory card pins that I would use as donor cart, given the tutorial linked above also provided the equivalence table for the SD card pins:

SD Card  |  Memory Card
------------------------
    1    |      9
    2    |      5
    3    |    2 or 10
    4    |      4
    5    |      11
    6    |    2 or 10
    7    |      7

+ Memory Card Pins 1 and 12 needs to be wired

After that I came across another diagram that suggested the addition of an activity LED for the data line between Memory card pins 6 (VSS2/Earth) and 7 (Data Line 0).

I could not resist the complimentary additional rice.

Now I can load my .dol files, and I have more blinking LED stuff. What a great double WIN evening it is.

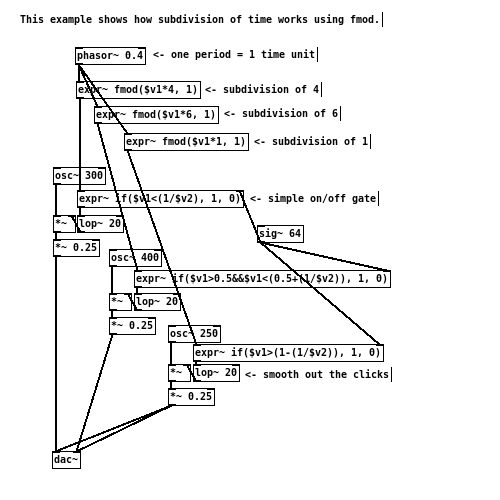
Time units, here refers to the duration of one single musical event. It is relative, in that a selected unit can be subdivided into smaller parts, as well as summed up to form a larger section. That is to say, if the time unit is measured in quarter notes, the sum of four units will make up for one bar, and half of the unit would be an eighth note. If the time unit were expressed as one bar, four of which together could resolve to a musical phrase, and a semiquaver would be one sixteenth of the unit duration.

To understand timing in this manner is extremely helpful when making compositional arrangements using DSP control signals. As long as one is able to express the required timing in terms of proportions relating the chosen time units, simple arithmetic would be all it takes to implement the solution.

For instance, if one period of a sawtooth wave is considered as one bar, to produce the same waveform but at the rate of quarter notes would simply be:

[phasor~ 1]->[expr~ fmod($v1*4, 1)]->[send~ QTR_NOTES]
           \
            ->[send~ ONE_BAR]

This works by first multiplying the original signal with an desired amount, in order to scale up the “rate of change” appropriately. It is then passed through the fmod (Floating Point Modulo) function. By having the second argument set to 1, fmod essentially discard the integer portion of its input. This results to a signal which has the amplified increment, but restricted to floating point values between 0 and 1.

To gain any other subdivisions of one bar at 1Hz, simply replace the multiplication factor with another value. Thus, one can quickly produce multiple and parallel timing signal from just one [phasor~] object.

However, if one period of a sawtooth is decided to be one beat (quarter notes, for example), to obtain the timing signal for one bar and beyond would require a little more thought, but otherwise based on the same principle as above.

[phasor~ 0.25]->[expr~ fmod($v1*4,1)]->[send~ QTR_NOTES]
              \
               ->[send ONE_BAR]

This works by first dividing the frequency of the starting [phasor~ ] object, to reduce its rate by an appropriate amount (in this case, 4 times slower). The slowed down oscillator can then be used as the “extended” timing. But, to regain the sawtooth of 1Hz as one beat, the same fmod trick is again used.

In short, subdividing a given time unit does not change the frequency of the original control signal. Whereas timing extension involves reducing the frequency of the initial control oscillator.

Get the source here

Exercise:

• All the examples above measures time in Hz (1 period of 1Hz is 1 second long), how could this be translated to use more conventional measurement such as BPM?

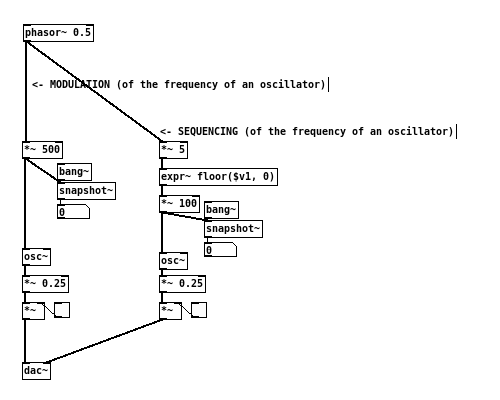
Apart from the discrete changes in values, generating control signals for sequencing, can be approached just the same way as that for modulation. That is to say, one essentially find ways to “alter” the appearance of a given waveform so that a “stepped” version of it emerges as a result. Transforming a signal from continuously and smoothly changing to being quantised and value-restricted is therefore the objective when preparing control signals for sequencing.

The following quick example will produce a sawtooth signal that contains 10 distinct steps within its wave cycle.

[phasor~ 1]->[expr~ floor($v1*10, 0)/10]

Because a quantised signal holds the same value temporarily until the next element comes along, by using comparison operators (“equals for example”), it becomes possible to isolate/select a certain portion of the sequence. Since the comparative statements will return true for the entire duration of given time “step”, it thus allow for further (differential) treatments to the signal that falls on either side of the test. This property of the sequencing signal might initially seem trivial, but it makes such a signal very useful in solving many of the tasks that are commonly faced when dealing with time dependent structures.

The following example demonstrates how one can select the last element in the sequence of 4 incremental counts (0,1,2,3,0,1,2,3…), and subsquently reassign its output value (0,1,2,0,0,1,2,0…).

[phasor~ 1]->[expr~ floor($v1*4, 0)]->[expr~ if($v1 == 3, 0, $v1)]

Combining with relational tests, control signal for sequencing can extend far beyond as being a simple counting mechanism. Many common objects such as [select], [spigot], [int] and [moses] can all be emulated easily. Dynamic signal routing and flexiable looping are other examples that are relatively uncomplicated to implement.

The exmple below demonstrates an interesting way of counting by utilising the modulo function.

Get the source here

Exercise:

What other arithmetic functions can be used to modify the control signal?

Which other parts of the example patch can be modulated/sequenced?

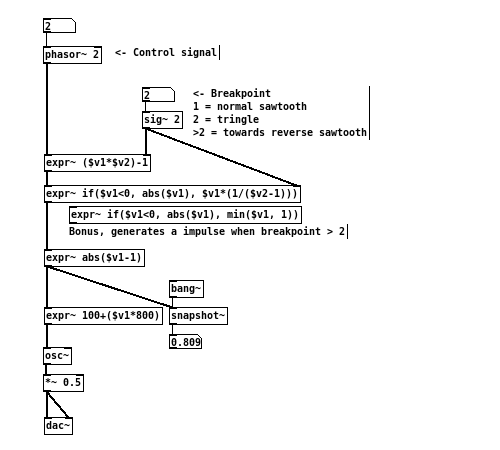
Modulation, can essentially be seen as applying the “shape” of one signal onto another. For example, modulating the amplitude of an oscillator (carrier signal) with an sawtooth wave (modulating/control signal) would create a crescendo in loudness with a sudden drop in volume at the end. Triangle wave, on the other hand would produce a crescendo and followed by a smooth decrescendo. The resulting sound thus follows the visual appearance of the modulating signal.

Visualising the control signal in such a manner can be quite a intuitive process when applying modulations in composition.

Supposing the control signal always starts with a sawtooth wave ([phasor~]), the aim therefore is to find ways to “bend” its linear ramp into other suitable/interesting shapes to be further made used of. Following examples will demonstrate some simple transformations in which a sawtooth wave is “shaped” into other useful waveforms.

• Reverse Sawtooth:

  [phasor~ 1]->[-~ 1]->[abs~]

• Triangle wave:

  [phasor~ 1]->[*~ 2]->[-~ 1]->[abs~]

• Square/Pulse wave:

  [phasor~ 1]->[expr~ if($v1<0.5, 1, 0)]

• Attack/Decay envelope:

  

Above examples may seem trivial at first, they do however provide highly functional shapes that can be very useful in many common compositional scenarios.

Exercise:

Use only [expr~] object to reverse Sawtooth and Triangle wave

The Triangle wave above is not entirely correct, how can it be fixed?

How to do simple Pulse Width Modulation from the given example above?

Modulation and sequencing are two building blocks that are fundamental to sound synthesis and music making. The former typically aims to control the finer details and the timbre of a sound, whereas the latter deals with the arrangement and the structure of “musical” events over time. Their definitions can briefly be summarized as the following:

Modulation, applying a continuous signal onto a parameter, so the value of the parameter changes smoothly over time.

Sequencing, applying a sequence of values onto a parameter, so the value of the parameter changes discretely over time.

Modulation is generally easier to understand, as it often is taught as the “introduction” to sound synthesis. The three properties of any given oscillating sound (frequency, amplitude and phase) can all be modulated to create interesting results.

Sequencing, on the other hand, is less common to achieve using digital audio signal exclusively. The objective is essentially to quantize the signal into discrete “steps”. As a result, even though the signal is continuous, the changes in its values are quantized accordingly. One can also think of it as the reduction in “resolution” of a given signal. One example would be to make a DSP version of a step counter.

The “trick” to make such a counter is simply to multiply the signal with a (max count) variable, and then only to take the integer part of the result. For example:

[phasor~ 1]->[*~ 5]->[expr~ floor($v1, 0)]

This will result to a signal that counts from 0 to 4 in one second.

Having a good practical understanding on both modulation and sequencing is crucial in grasping and taking full advantage of the topics to come. The following questions can be used as starting points to approach the subject.

What are the differences and commonalities between modulation and sequencing?

Are they essentially the same?

Where can they be applied?

EXAMPLE PATCH: 001_mod-seq.pd

Get the source here

Edit: replaced int(reg) with int(round(reg)). Not that it should have any noticeable sound differences, but it’s a bit more accurate.

Resuming.

In order to play a scale, I needed notes. But the GBA sound chip has no clue what a note is, it just want to be fed with the right register value to control the frequency of a specific channel. The register value can be calculated with 2048 – 4194304 / (32 * frequency), then converted to hexadecimal. So far I calculated this manually to get a few octaves of C and G notes.

In order to play several scales, I need now much more notes and I’m not going to calculate them all by hand, nor make the poor GBA CPU do that in real-time every time a note needs to be played.

So it’s time for some high-level laziness:

#!/usr/bin/env python

notes = [["C",65.406],["CH",69.296],["D",73.416],["DH",77.782],
["E",82.407],["F",87.307],["FH",92.499],["G",97.999],
["GH",103.826],["A",110],["AH",116.541],["B",123.471]]

def makeHex(freq):
    reg = 2048-(4194304/(32*freq))
    regHex = "{0:#0{1}x}".format(int(round(reg)),6)
    return regHex

def makeArray(note,freq):
    i = 0
    array = "int "+note+" [6] = {"
    while i < 6:
        array += makeHex(freq*pow(2,i))+","
        i += 1
    return array[:-1]+"};"

for note in notes:
    print makeArray(note[0],note[1])

This thing will produce the following that I can then nicely paste in my C code, Ô pythonesque joy and wonders:

int C [6] = {0x002c,0x0416,0x060b,0x0706,0x0783,0x07c1};
int CH [6] = {0x009d,0x044e,0x0627,0x0714,0x078a,0x07c5};
int D [6] = {0x0107,0x0483,0x0642,0x0721,0x0790,0x07c8};
int DH [6] = {0x016b,0x04b5,0x065b,0x072d,0x0797,0x07cb};
int E [6] = {0x01c9,0x04e5,0x0672,0x0739,0x079d,0x07ce};
int F [6] = {0x0223,0x0511,0x0689,0x0744,0x07a2,0x07d1};
int FH [6] = {0x0277,0x053b,0x069e,0x074f,0x07a7,0x07d4};
int G [6] = {0x02c7,0x0563,0x06b2,0x0759,0x07ac,0x07d6};
int GH [6] = {0x0312,0x0589,0x06c4,0x0762,0x07b1,0x07d9};
int A [6] = {0x0359,0x05ad,0x06d7,0x076c,0x07b6,0x07db};
int AH [6] = {0x039b,0x05ce,0x06e7,0x0773,0x07ba,0x07dd};
int B [6] = {0x03da,0x05ed,0x06f7,0x077b,0x07be,0x07df};

Then I guess I can find a way to assign the tonic and dominant notes on the fly depending on the selected scale… Mmmm… we’ll see about that in the next part I suppose.

Making some progress. Next to the noise channel, the software is now also using the three other legacy DMG sound generators (two square wave generators and a 4-bit DAC wave generator).

As for the generative part, this lullaby relies on a 6/8 time signature and only use dominant and tonic notes for the square parts. Every sound generator loops through their respective six steps sequences, that are populated pseudo randomly, following some basic constraints:

– Sound channel 1: randomly picking different octaves of the dominant and tonic notes of the given scale, with some muting every now and then, except on step 0 and 3, that are on all the time.

– Sound channel 2: same with a longer envelope and always muted on steps 1, 2, 4 and 5.

– Sound channel 3: whenever new sequences are generated, two WAV RAM banks are filled with four chunks of random 4-bit crap (in fact I just fill it entirely with 16-bit crap at once, that’s more fancy), and the 6 steps are just randomly populated with 0s and 1s which then determine which bank is played. As for the playback frequency, this is basically one of notes from the given scale for the whole duration of the sequence.

At the moment I’m still using the Hungarian minor scale, but starting to think that if it would be nice to have few more available. It sounds like this :

(still from emulation at this point)

Yes it’s possible to compile devkitPro/devkitARM on FreeBSD. It does require a bit of tweaking though. Below are some notes I took while compiling devkitARM release 42 and associated libraries on FreeBSD 10.0-STABLE. It’s a lot of quick hacks, but that worked out for having a fully working libga based environment.

* bash script does not work
  -> replace /bin/bash with more portable /usr/bin/env bash
* GNU MP is needed
  -> portmaster math/gmp
* gmp header files not found while GCC is compiled
  -> problem files need manual editing pointing to the full path
  of the header, for instance /usr/local/include/gmp.h
* linker cannot find -lmpc at the end of stage 1 GCC build
  -> -I/usr/local/include -L/usr/local/lib needs to be added
  in .devkitARM/arm-none-eabi/gcc/gcc/Makefile
* abort defined twice in a row in libsysbase abort.c
  -> I removed the duplicate lines
* same with iosupport.c ?
* same with close.c, environ.c, execve.c, etc
  OK something is definitively wrong with the distribution of this
  source, or one of the scripts. I ended up `for ... do`-ing a lot
  of mv commands.
* libfreeimage missing for building grit-0.8.12
  -> portmaster graphics/freeimage
* grit configure cannot find libfreeimage
  -> configure/configure.ac modified to skip test
  and -I/usr/local/include -L/usr/local/lib
* grit fails to compile because cannot find FreeImage.h
  -> relevant .h and .cpp files edited to 
  include /usr/local/include/FreeImage.h
* tar tap error with libnds, libmirko, and maybe another one
  -> add '-f -' to relevant Makefile:
  bzip2 -cd libnds-$(VERSION).tar.bz2 | \
  tar -x -f - -C $(DEVKITPRO)/libnds
* Maxmod fails to build
  ->replace @make with gmake in maxmod.mak
* Examples installed manually
* when compiling projects, clang is used, fails
  -> the Makefile needs editing to replace @make with gmake

It’s very rough, but should give enough hints.

There is a small thread on the DevkitPro/DevkitARM forum on the matter: http://devkitpro.org/viewtopic.php?f=2&t=3203

Sooooo… 0xA is still alive I guess… :)

I’m currently working on a small GBA ROM for an upcoming net release compilation that has the lullaby for theme. The idea is to make a small software that will create lullaby-esque sequences using the 4 legacy DMG sound channels of the GBA. That’s a good excuse to get into DevkitARM, although now I’m thinking that it might have been good to learn GBDK to make a GB ROM instead. Ah well, can’t be bothered to restart and maybe I can use the opportunity to add some graphics.

So far the software is tuned for the Hungarian scale in C, which makes a very dramatic lullaby somehow, I’ll tune later on. It was quite straightforward, the most delicate part being the sound registers, but thanks to belogic everything is super well documented. In a nutshell, it’s all about bitmasking and feeding the right registers with 16bit words.

For instance a simple way to control the noise channel can be made like this:

int setSnd4(int cd, int sta, int stp, int ti, int re)
{
    // DMG Channel 4 Noise parameters, reset and loop control
    // See specs: http://belogic.com/gba/registers.shtml#REG_SOUND4CNT_H
    //
    // cd    -- Clock divider frequency (0-7)
    // sta   -- Counter stages (0-1), 15 or 7
    // stp   -- Counter Pre-Stepper frequency (0-15)
    // ti    -- Timed mode (0-1), continuous or timed
    // re    -- Sound reset

    return (re << 15) | (ti << 14) | (stp << 4) | (sta << 3) | cd;
}

int playNote4(int noise)
{  
    REG_SOUND4CNT_L=0xA100;
    REG_SOUND4CNT_H=noise;

    return 0;
}

playNote4(setSnd4(2,1,10,0,1));

That’s just basic copypasta to get the idea. Once it is sequenced and populated with random values, it sounds like this:

Note: this is recorded from an emulator, too lazy to flash it. Yawn. Sleep. Bye.

Chun Lee will be at the Linux Audio Conference, giving a workshop on DSP based music composition methodology. See the full schedule here.