______                     
                 /      |       ________     
                /       |____  /        \    
               /        |    \/   _      \   
               \       ___       /_\      \  
                \      \_/          .      \ 
                 \          /\_____/       / 
                  \________/      |       /  
                                  |______/   

[THE_EXPR_METHOD] 012 Trapezoid

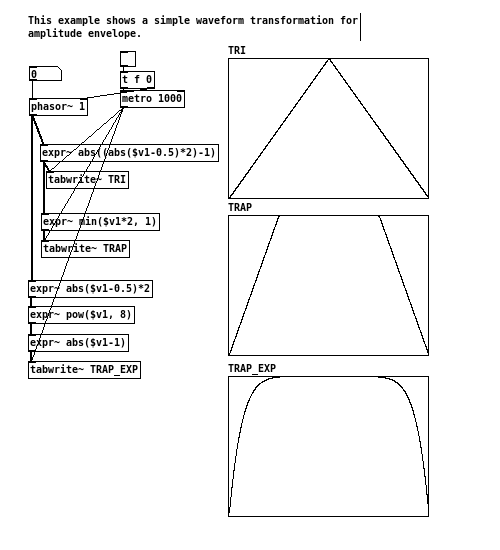
Some wave forms, like sawtooth, are easy to implement and provides useful building blocks in signal manipulation. Trapezoid is another such example.

It is particularly suitable used as amplitude envelope, in which smooth attack and decay can be guaranteed, whilst the “on” portion of the envelope stays fully open for as long as possible. For instance, if an triangle wave had been used, the envelope will never stay fully open, as the signal starts to ramp down as soon as it reaches the top. As a result, modulated signal can appear to be continuously fading in and out, or the lost of overall “loudness”. Trapezoid, on the other hand, provides an convenient method to address these issues.

Trapezoid, in fact, can be easily constructed out of a triangle wave, with two additional operates involved. The triangle is first scaled up (multiplication) by a desirable amount, and than clipped(min()) at the maximum y-axis value of the envelope, which conventionally is 1. The more the signal is scaled, the steeper the sides of the resulting trapezoid becomes, thus shorter in attack/decay duration.

One other variation would be to use the pow() function, turning the liner slopes of the (inverted) triangle into exponential curves. The envelope is then flipped over to the right orientation for use. The advantage of this method is that, given the same breakpoint locations, the total “on” area of the signal would be larger than that of the linear trapezoid. The resulting modulation would have even less perceived loudness loss. However, such a shape resembles more of a classic jello than a trapezoid.

In the previous post on sample play back, where a given sound file are splitted into multiple sections, clipping can often occur at the edges of the segments due to non zero-crossing. This is an ideal scenario to apply trapezoid, or equivalent variants, to rectify such error, by using it as a amplitude envelope.

Get the source here

Exercise:

• Are there other types of slops/curves that can be used in the waveform transformation similar to the exmple above?